Câu 1. Cho hàm số \( y = f(x) \) có đồ thị như hình vẽ.

Gọi \( S \) là tổng diện tích của 2 vùng được gạch chéo. Khẳng định nào sau đây SAI?

Chọn: B

Page 1

Câu 2. Cho hàm số \( y = f(x) \) có đồ thị như hình vẽ. Giá trị của \( \int_{0}^{4} f(x) \, dx \) bằng:

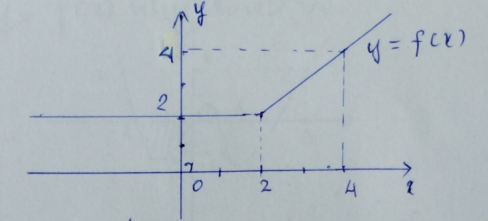
Lời giải:

\[ \int_0^4 f(x)\, dx = \int_0^2 f(x)\, dx + \int_2^4 f(x)\, dx = 2 \times 2 + \frac{(4 + 2)\times 2}{2} = 4 + 6 = 10 \]

Chọn: D

Page 2

Câu 3. Cho hàm số \( y' = f(x) \) có đạo hàm trên \( \mathbb{R} \), đồ thị hàm số \( y = f(x) \) như hình vẽ.

Biết diện tích hình phẳng phần sọc kẻ bằng 3. Tính giá trị của biểu thức: \( T = \int_{1}^{3} f'(x) \, dx + 2 \int_{-2}^{0} f(x) \, dx \)

Lời giải:

\( T = \left. f(x) \right|_{1}^{3} + 2 \times 3 = f(3) - f(1) + 6 = 2 - (-1) + 6 = 9 \)

Chọn: C

Page 3

Lời giải:

Ta có: \( \int_0^4 f(x) \, dx = F(4) - F(0) = F(4) - G(0) + a \)

\( \Rightarrow G(0) - F(0) = a \)

Mặt khác: \( F(x) \) và \( G(x) \) là hai nguyên hàm của cùng một hàm số \( f(x) \)

\( \Rightarrow G(x) = F(x) + k, \ \forall x \in \mathbb{R} \)

Suy ra \( G(x) = F(x) + a \Rightarrow G(x) - F(x) = a \)

Vì \( \int_0^4 |G(x) - F(x)| \, dx = \int_0^4 a \, dx = a \left. x \right|_0^4 = 4a =20\)

\(\Rightarrow a = 5 \)
 

Chọn: B

Page 4

Câu 5. Cho hàm số \( y = \dfrac{1}{2}x^2 \). Gọi \( S_1, S_2 \) là diện tích của hai phần trong hình vuông và được gạch chéo như hình vẽ.

Khi đó tỉ số \( \dfrac{S_1}{S_2} \) bằng:

Lời giải:

\( S_2 = \int_0^2 \dfrac{x^2}{2} \, dx = \left. \dfrac{x^3}{6} \right|_0^2 = \dfrac{8}{3} \)

\( S_1 = 4 - S_2 = 4 - \dfrac{4}{3} = \dfrac{8}{3} \)

\( \Rightarrow \dfrac{S_1}{S_2} = \dfrac{8/3}{4/3} = 2 \)

Chọn: C

Page 5

Câu 6. Cho hình phẳng (H) giới hạn bởi các đường \( y = x^2 \), \( y = 0 \), \( x = 0 \), \( x = 4 \). Đường thẳng \( y = k \) với \( 0 < k < 16 \) chia (H) thành hai phần có diện tích \( S_1, S_2 \) như hình vẽ.

Tìm \( k \) để \( S_1 = S_2 \).

Lời giải:

Ta có: \( S_1 + S_2 = \int_0^4 x^2 \, dx = \left. \frac{x^3}{3} \right|_0^4 = \frac{64}{3} \)

Đồ thị hàm số \( y = x^2 \) cắt đường \( y = k \) tại các điểm có hoành độ là nghiệm của phương trình:

\( x^2 = k \Leftrightarrow x = \pm \sqrt{k} \)

Khi đó:

\( S_2 = \int_0^{\sqrt{k}} x^2 \, dx + \int_{\sqrt{k}}^4 k \, dx = \left. \frac{x^3}{3} \right|_0^{\sqrt{k}} + k(4 - \sqrt{k}) \)

\( = \frac{k\sqrt{k}}{3} + k(4 - \sqrt{k}) = 4k - \frac{2}{3}k\sqrt{k} \)

Để \( S_1 = S_2 \Rightarrow S_2 = \frac{32}{3} \Rightarrow 4k - \frac{2}{3}k\sqrt{k} = \frac{32}{3} \)

\( \Leftrightarrow 12k - 6k +16 = 0 \Leftrightarrow \sqrt{k} = 2 \Rightarrow k = 4 \)

(Vì \( x^3 - 6x^2 + 16 = (x - 2)(x^2 - 4x + 8) \))

Vậy \( k = 4 \)

Chọn: D

Page 6

Câu 7. Cho hàm số \( y = f(x) \) có đồ thị hàm số \( y' = f'(x) \) như hình vẽ.

Giá trị \( \min f(x) \) trên đoạn \([-3;2]\) bằng:

Lời giải:

Từ đồ thị của hàm số \( y' = f'(x) \), ta suy ra bảng biến thiên của hàm số \( y = f(x) \)

Để tìm \( \min f(x) \) trên đoạn \( [-3;2] \), cần so sánh \( f(-3) \) và \( f(0) \)

Xét: \( \int_{-3}^{0} f'(x) \, dx = S_3 - S_2 > 0 \)

Mặt khác: \( \int_{-3}^{0} f'(x) \, dx = f(0) - f(-3) \Rightarrow f(0) - f(-3) > 0 \Rightarrow f(0) > f(-3) \)

Vậy \( \min f(x) = f(-3) \) trên đoạn \( [-3;2] \)
 

Chọn: D

Page 7

Lời giải:

\( V = \pi \int_1^2 (y^2 \, dx = \pi \int_1^2 x \, dx = \pi \left. \frac{x^2}{2} \right|_1^2 = \frac{\pi}{2}(4 - 1) = \frac{3\pi}{2} \)

Chọn: B

Page 8

Lời giải:

 \( 4 - x^2 = 0 \Rightarrow x = \pm 2 \)

\( V = \pi \int_{-2}^{2} (4 - x^2)^2 \, dx = \pi \int_{-2}^{2} (16 - 8x^2 + x^4) \, dx \)

\( = \pi \left( \int_{-2}^{2} 16 \, dx - 8 \int_{-2}^{2} x^2 \, dx + \int_{-2}^{2} x^4 \, dx \right) \)

\( = \pi \left( 16x - \frac{8x^3}{3} + \frac{x^5}{5} \right) \Bigg|_{-2}^{2} = \frac{512\pi}{15} \)

Chọn: A

Page 9

Lời giải:

* \( x^2 - 4x + 6 = -x^2 - 2x + 6 \)

\(\Leftrightarrow 2x^2 - 2x = 0  \Rightarrow \begin{cases} x = 0 \\ x = 1 \end{cases} \)

\( V = \pi \int_0^1 \left| (x^2 - 4x + 6)^2 - (-x^2 - 2x + 6)^2 \right| dx \)

\( = \pi |\int_0^1 \left[ (x^2 - 4x + 6)^2 - (-x^2 - 2x + 6)^2 \right] dx| \)

\( = 3\pi \)

Chọn: C

Page 10