Bài giải:

\( f'(x) = 6x^2 + 6x = 6x(x+1) = 0 \Leftrightarrow \left[ \begin{array}{l} x = 0 \\ x = -1 \end{array} \right. \)

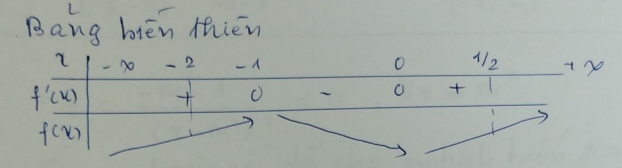
\( \max\limits_{[-2;\ \tfrac{1}{2}]} f(x) = \max\left\{ f(-1), f\left( \tfrac{1}{2} \right) \right\} = \max\{0,\ 0\} = 0 \)
\( \min\limits_{[-2;\ \tfrac{1}{2}]} f(x) = \min\left\{ f(-2), f(0) \right\} = \min\{-5,\ -1\} = -5 \)

\( P = M - m = 0 - (-5) = 5 \)

Chọn: A

Page 1

---

Bài giải:

\( y' = \dfrac{-m^2 - 1}{(x - m^2)^2} < 0, \forall x \ne m^2 \)

Suy ra hàm số đã cho nghịch biến trong \( [-3; -2] \) (vì \( m^2 \notin [-3; -2] \))

Nên \( \min y_{[-3, -2]} = f(-2) = \dfrac{-1}{-2 - m^2} = \dfrac{1}{m^2 + 2} \)

Chọn: A

Page 2

---

Bài giải:

Tập xác định: \( D = \mathbb{R} \setminus \{0\} \)

\( f'(x) = 1 - \dfrac{4}{x^2} = \dfrac{x^2 - 4}{x^2} = 0 \Leftrightarrow x = \pm 2 \)

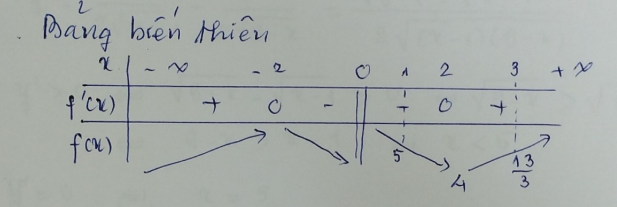
\( \min\limits_{[1;\ 3]} f(x) = 4 \quad \text{và} \quad \max\limits_{[1;\ 3]} f(x) = 5 \)

\( \min\limits_{[1;\ 3]} f(x) \cdot \max\limits_{[1;\ 3]} f(x) = 4 \cdot 5 = 20 \)

Chọn: B

Page 3

---

Bài giải:

Tập xác định của hàm số: \( D = [1; 9] \)

\( y' = \frac{1}{2\sqrt{x - 1}} - \frac{1}{2\sqrt{9 - x}} = \frac{\sqrt{9 - x} - \sqrt{x - 1}}{2\sqrt{(x - 1)(9 - x)}} \)

\( y' > 0 \Leftrightarrow \sqrt{9 - x} - \sqrt{x - 1} > 0 \Leftrightarrow \sqrt{9 - x} > \sqrt{x - 1} \)

\( \Leftrightarrow 9 - x > x - 1 \Leftrightarrow x < 5 \)

\( y' = 0 \Leftrightarrow x = 5 \)
 

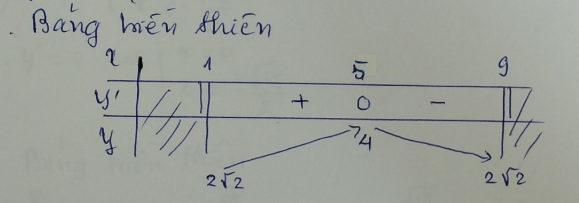
Do đó: \( M = 4 \), \( m = 2\sqrt{2} \)

Suy ra \( T = 4 + 4 = 8 \)

Chọn: C

Page 4

---

Bài giải:

Điều kiện: \( 4 - x^2 \geq 0 \Leftrightarrow -2 \leq x \leq 2 \Rightarrow D = [-2; 2] \)

\[ y' = 2x - \frac{2x}{2\sqrt{4 - x^2}} = \frac{x(2\sqrt{4 - x^2} - 2)}{\sqrt{4 - x^2}} \]

Xét dấu \( y' \):

\( y' > 0 \Leftrightarrow x > 0 \) và \( \sqrt{4 - x^2} > 1 \Rightarrow x^2 < \frac{15}{4} \)

\( y' < 0 \Leftrightarrow x < 0 \) và \( \sqrt{4 - x^2} > 1 \Rightarrow x^2 < \frac{15}{4} \)

\( y' = 0 \Leftrightarrow x = \pm \frac{\sqrt{15}}{2} \)

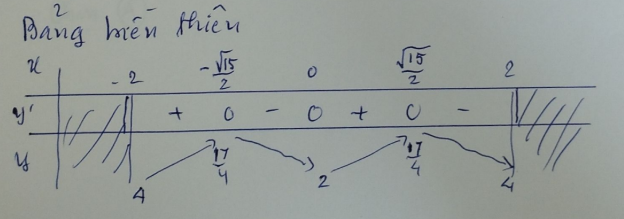
Ta có: \( M = \dfrac{17}{4} \), \( m = 2 \)

\( M + m = \dfrac{17}{4} + 2 = \dfrac{25}{4} \)

Chọn: D

Page 5

---

Bài giải:

Đặt \( t = 2^x \Rightarrow 2 \leq t \leq 4 \)

\[ y = \dfrac{2^x + 2m}{2^{x+1} + 3} = \dfrac{t + m}{2t + 3} \]

\[ y' = \dfrac{3 - 2m}{(2t + 3)^2} \]

Xét các trường hợp để \( \min y = \min f(t) = 1 \) trên \( [2, 4] \):

1. \( 3 - 2m > 0 \Rightarrow m < \dfrac{3}{2} \)

\( f(2) = \dfrac{2 + m}{7} = 1 \Rightarrow m = 5 \)

2. \( 3 - 2m < 0 \Rightarrow m > \dfrac{3}{2} \)

\( f(4) = \dfrac{4 + m}{11} = 1 \Rightarrow m = 7 \)

3. \( 3 - 2m = 0 \Rightarrow m = \dfrac{3}{2} \Rightarrow \) không phù hợp

Chọn: A

Page 7

---

Bài giải:

\[ y' = 3x^2 - 6x - 9 = 0 \Leftrightarrow x = -1, x = 3 \]

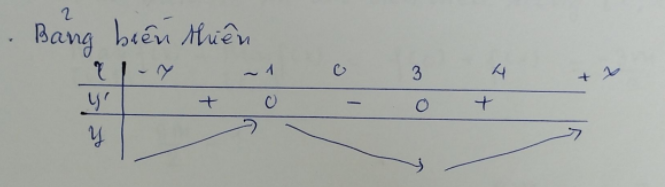
\( \min y = f(3) = -27 + m = -25 \Rightarrow m = 2 \)

\( P = 2m + 1 = 2 \cdot 2 + 1 = 5 \)

Chọn: D

Page 8

---

Bài giải:

\[ y' = \dfrac{-2 - 3m}{(x - 2)^2} \Rightarrow \text{Hàm số đồng biến hay nghịch biến phụ thuộc vào dấu của tử số} \]

Vì hàm số đồng biến hoặc nghịch biến trên \( [0; 1] \), ta xét: \[ \max y + \min y = f(0) + f(1) = \dfrac{3m}{-2} + \dfrac{1 + 3m}{-1} = -\dfrac{3m}{2} - (1 + 3m) \]

\[ = -\dfrac{3m}{2} - 1 - 3m = -\dfrac{9m}{2} - 1 \]

Cho tổng bằng 7: \[ -\dfrac{9m}{2} - 1 = 7 \Rightarrow m = -\dfrac{16}{9} \Rightarrow m \in (-2; -1) \]

Chọn: D

Page 9

---

Bài giải:

Tập xác định của hàm số: \( D = [-1; +\infty) \)

\[ f'(x) = \dfrac{1}{2} - \dfrac{1}{2\sqrt{x+1}} = \dfrac{\sqrt{x+1} - 1}{2\sqrt{x+1}} \]

\( f'(x) > 0 \Leftrightarrow \sqrt{x+1} - 1 > 0 \Leftrightarrow x > 0 \)

\( f'(x) = 0 \Leftrightarrow x = 0 \)

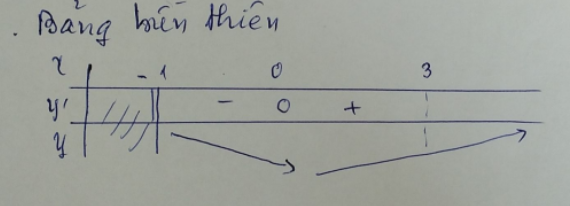
Giá trị lớn nhất trên đoạn \( [0; 3] \):

\( M = \max f(x) = f(3) = \dfrac{3}{2} - 2 = -\dfrac{1}{2} \)

Giá trị nhỏ nhất trên đoạn \( [0; 3] \):

\( m = \min f(x) = f(0) = -1 \)

Tổng \( S = 3m + 2M = 3(-1) + 2\left(-\dfrac{1}{2}\right) = -3 - 1 = -\dfrac{7}{2} \)

Chọn: A

Page 10

---