Tính đơn điệu của hàm số

Beedemy

Trang chủ

Bài viết

Tính đơn điệu của hàm số - Bài kiểm tra

Câu 1. Hàm số nào dưới đây nghịch biến trên \( \mathbb{R} \)

A. \( y = -x^3 + x \)

B. \( y = -x^4 - x^2 \)

C. \( y = -x^3 - x \)

D. \( y = x^4 - 2x^2 + 5 \)

Lời giải:

Chọn: C vì \( y' = -3x^2 - 1 < 0, \ \forall x \in \mathbb{R} \)

Page 1

Câu 2. Cho hàm số \( y = f(x) \) có đồ thị như hình vẽ

Khẳng định nào sau đây đúng?

A. \( f'(-2) > 0, \quad f'(0) > 0 \)

B. \( f'(-2) > 0, \quad f'(0) < 0 \)

C. \( f'(-2) < 0, \quad f'(0) > 0 \)

D. \( f'(-2) < 0, \quad f'(0) < 0 \)

Lời giải:

Chọn: B vì một khoảng nhỏ chứa -2 hàm số đồng biến và một khoảng nhỏ chứa 0 hàm số nghịch biến

Page 2

Câu 3. Cho hàm số \( y = -x^3 - mx^2 + mx + 9 \), \( m \) là tham số. Có bao nhiêu giá trị nguyên của \( m \) để hàm số nghịch biến trên \( \mathbb{R} \)?

A. 4

B. 1

C. 2

D. 3

Lời giải:

Hàm số đã cho nghịch biến trên \( \mathbb{R} \)
\( \Leftrightarrow y' = -3x^2 - 2mx + m \leq 0, \ \forall x \in \mathbb{R} \)
\( \Leftrightarrow \Delta = m^2 + 3m \leq 0 \)
\( \Leftrightarrow -3 \leq m \leq 0 \)

\( (m \in \mathbb{Z} : m = -3, -2, -1, 0) \)

Chọn: A

Page 3

Câu 4.: Cho hàm số \( y = f(x) \) có đạo hàm \( f'(x) = 2x^2 + 1 \), \( \forall x \in \mathbb{R} \). Khẳng định nào dưới đây đúng?

A. \( f(0) > f(1) \)

B. \( f(1) < f(4) \)

C. \( f(2) > f(5) \)

D. \( f(-1) > f(1) \)

Lời giải:

\( f'(x) = 2x^2 + 1 > 0, \ \forall x \in \mathbb{R} \)
Suy ra hàm \( f \) đồng biến trên \( \mathbb{R} \).
Chọn: B

Page 4

Câu 5. Cho hàm số \( y = f(x) \) có đạo hàm \( f'(x) = x^2( x-1) \), \( \forall x \in \mathbb{R} \). Hàm số \( g(x) = f(x^2) \) nghịch biến trên khoảng nào dưới đây?

A. \( (-1; 0) \)

B. \( (0; 1) \)

C. \( (-\infty; 0) \)

D. \( (1; +\infty) \)

Lời giải:

\( g'(x) = 2x f'(x^2) = 2x \cdot x^4 (x^2 - 1) = 2x^5 (x - 1)(x + 1) \)

Bảng biến thiên của hàm số \( y = g(x) \)

Chọn: B

Page 5

Câu 6. Cho hàm số \( y = f(x) \) có đồ thị như hình vẽ

Hàm số \( g(x) = 2025 - f(x) \) đồng biến trong khoảng nào?

A. \( (1; 2) \)

B. \( (3; 4) \)

C. \( (-2; 1) \)

D. \( (-1; 1) \)

Lời giải:

\( g'(x) = -f'(x) > 0 \Leftrightarrow f'(x) < 0 \Leftrightarrow -1 < x < 1 \)

Vậy hàm \( g \) đồng biến trong \( (-1; 1) \).

Chọn: D

Page 6

Câu 7. Cho hàm số \( y = f(x) \) có đạo hàm \( f'(x) = (x - 1)(x - 2)^2(x - 3)^3(x - 4) \), \( \forall x \in \mathbb{R} \). Hàm số \( f(x) \) nghịch biến trong khoảng nào sau đây?

A. \( (-\infty; 1) \)

B. \( (3; 4) \)

C. \( (1; 3) \)

D. \( (4; +\infty) \)

Lời giải:

Bảng biến thiên của hàm \( f \)

Chọn: C

Page 7

Câu 8. Có bao nhiêu giá trị nguyên của \( m \) để hàm số \( y = \frac{mx - 6m + 5}{x - m} \) đồng biến trên khoảng \( (2; +\infty) \)?

A. 0

B. 1

C. 3

D. 2

Lời giải:

\( y' = \frac{-m^2 + 6m - 5}{(x - m)^2} \)

Hàm số đã cho đồng biến trong \( (2; +\infty) \)

\( \Leftrightarrow \left\{ \begin{array}{l} -m^2 + 6m - 5 > 0 \\ m \leq 2 \end{array} \right.
\Leftrightarrow \left\{ \begin{array}{l} 1 < m < 5 \\ m > 2 \end{array} \right.
\Leftrightarrow 1 < m \leq 2 \)

\( (m \in \mathbb{Z} : m = 2, 3, 4) \)

Chọn: B

Page 8

Câu 9. Tìm tất cả giá trị của \( m \) để hàm số \( y = \frac{1}{3}(m^2 - 2m)x^3 + mx^2 + 3x \) đồng biến trên \( \mathbb{R} \)

A. \( m \leq 0 \)

B. \( 1 < m \leq 3 \)

C. \( \left[ \begin{array}{l}
m \leq 0 \\
m \geq 3
\end{array} \right. \)

D. \( \left[ \begin{array}{l}
m < 0 \\
m \geq 3
\end{array} \right. \)

Lời giải:

\( y' = (m^2 - 2m)x^2 + 2mx + 3 > 0, \ \forall x \in \mathbb{R} \) (1)

+ \( m^2 - 2m = 0 \Leftrightarrow \left[ \begin{array}{l} m = 0: \ y' = 3 \ (\text{thoả}) \\ m = 2: \ y' = 4x + 3 \ \text{không thỏa} \end{array} \right. \)

\( m^2 - 2m \ne 0 \)

\( \Leftrightarrow \left\{ \begin{array}{l} m < 0 \ \vee \ m > 2 \\ -2m^2 + 6m \leq 0 \end{array} \right.
\Leftrightarrow \left\{ \begin{array}{l} m < 0 \ \vee \ m > 2 \\ m \leq 0 \ \vee \ m \geq 3 \end{array} \right. \)

\( \Leftrightarrow \left[ \begin{array}{l} m > 0 \\ m \geq 3 \end{array} \right. \)

Tóm lại: \( \left[ \begin{array}{l} m \leq 0 \\ m \geq 3 \end{array} \right. \)

Chọn: C

Page 9

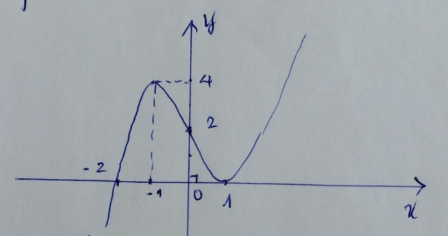
Câu 10. Cho hàm số \( y = f(x) \). Đồ thị của hàm số \( y = f(x) \) như hình dưới:

Hàm số \( y = f(x) - 2x + 3 \) đồng biến trên khoảng nào?

A. \( (-\infty; -2) \)

B. \( (-1; 0) \)

C. \( (-1; 1) \)

D. \( (-1; +\infty) \)

Lời giải:

\( g(x) = f(x) - 2x + 3 \Rightarrow g'(x) = f'(x) - 2 \)

\( g'(x) > 0 \Leftrightarrow f'(x) > 2 \Leftrightarrow \left[ \begin{array}{l} a < x < 0 \ (-2 < a < -1) \\ x > b \ (b > 1) \end{array} \right. \)

Hàm số \( g(x) = f(x) - 2x + 3 \) đồng biến trong các khoảng:
• \( (a; 0) \) với \( -2 < a < -1 \)
• \( (b; +\infty) \) với \( b > 1 \)

Vì \( (-1; 0) \subset (a; 0) \)

Chọn B

Page 10