Đáp án
Bài tập: Cho điểm \( I(1, 0, 0) \) và đường thẳng \( \Delta: \frac{x-1}{1} = \frac{y-1}{2} = \frac{z+2}{1} \).
Viết phương trình mặt cầu \( (S) \) tâm \( I \) cắt đường thẳng \( \Delta \) tại 2 điểm \( A, B \) sao cho \( \Delta IAB \) đều. Bán kính bằng:
Viết phương trình mặt cầu \( (S) \) tâm \( I \) cắt đường thẳng \( \Delta \) tại 2 điểm \( A, B \) sao cho \( \Delta IAB \) đều. Bán kính bằng:
A. \( \frac{2\sqrt{15}}{3} \quad \) B. \( \frac{\sqrt{15}}{3} \quad \) C. \( \frac{\sqrt{6}}{3} \quad \) D. \( \frac{2\sqrt{6}}{3} \)
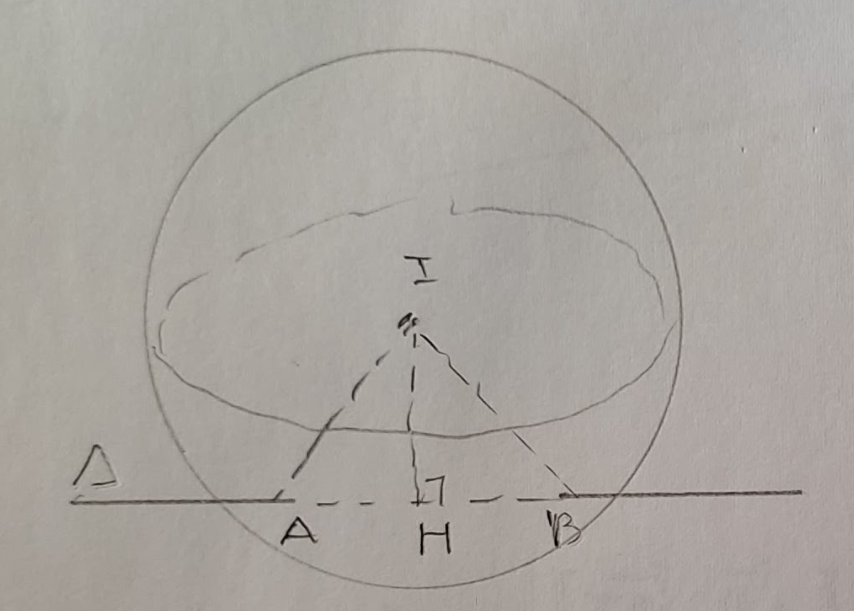
Đáp án:
\(\Delta\) qua \(M(1, 1, -2)\) và \(\vec{u}_\Delta = (1, 2, 1)\)
\( d(I, \Delta) = \frac{\left|[\vec{IM} , \vec{u}_\Delta]\right|}{|\vec{u}_\Delta|} = \sqrt{5} \)
\(\Delta IAB\) đều \(\iff IH = \frac{R\sqrt{3}}{2} = \sqrt{5} \iff R = \frac{2\sqrt{5}}{\sqrt{3}}\)
\((S): (x-1)^2 + y^2 + z^2 = \frac{20}{3} \Rightarrow \boxed{A}\)
\(\Delta IAB\) vuông?
\( d(I, \Delta) = \frac{R\sqrt{2}}{2} = \sqrt{5} \iff R = \sqrt{10} \)