Đáp án
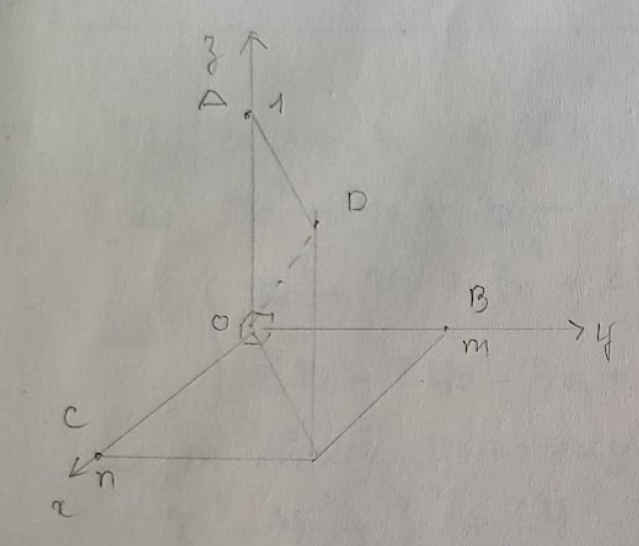
Bài tập: Trong không gian \( Oxyz \), cho \( A(0, 0, 1) \), \( B(0, m, 0) \), \( C(n, 0, 0) \), \( m, n \) là các số thực dương thỏa mãn: \( m + 2n = 1 \). Tính giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện \( OABC \).
\( A. \frac{\sqrt{6}}{4} \quad B. \frac{\sqrt{3}}{3} \quad C. \frac{\sqrt{30}}{10} \quad D. \frac{\sqrt{3}}{10} \).
Đáp án:
Gọi \( D(n, m, 1) \).
Tâm mặt cầu ngoại tiếp tứ diện \( OABC \) là tâm mặt cầu ngoại tiếp hình hộp có chứa các đỉnh \( O, A, B, C \), \( I \) là trung điểm của \( OD \): \( I\left(\frac{n}{2}, \frac{m}{2}, \frac{1}{2}\right) \).
Bán kính \( R \) của mặt cầu là: \( R = \frac{1}{2} \sqrt{n^2 + m^2 + 1} \)
\( 1 = m + 2n \leq \sqrt{5(m^2 + n^2)} \Rightarrow m^2 + n^2 \geq \frac{1}{5}\)
\( R = \frac{1}{2} \sqrt{m^2 + n^2 + 1} \geq \frac{1}{2} \sqrt{\frac{1}{5} + 1} = \frac{\sqrt{30}}{10} \)
\( \Rightarrow \min R = \frac{\sqrt{30}}{10} \Rightarrow \boxed{C} \)
(Dấu "=" xảy ra khi: \(m = \frac{n}{2}, \, n = 2m \Rightarrow \begin{cases} m = \frac{1}{5} \\ n = \frac{2}{5} \end{cases} \))