Bài tập: Viết pt mp (P) qua điểm \( M(1,3,2) \) vuông góc với mp \( Q: x - 2y - 2z + 1 = 0 \), sao cho \( d(O, \text{mp } P) = 1 \).  

A. \( \left[\begin{split} &4x + y + z - 9 = 0 \\ &2x - 3y + 5z - 3 = 0 \end{split} \right. \)  
B. \( \left[\begin{split} &2x + 2y - z- 6 = 0 \\ &2x + 3y - 2z - 7 = 0 \end{split} \right. \)  
C. \( \left[\begin{split} &2x - y + 2z - 3 = 0 \\ &2x + 11y - 10z - 15 = 0 \end{split} \right. \)  
D. \( \left[\begin{split} &2x - y + 2z - 1 = 0 \\ &2 - 3y + z + 6 = 0 \end{split} \right.\)  

Bài tập: Chứng minh: Viết pt mp \( D: ax + by + cz + d = 0 \). Mệnh đề nào sau đây đúng:  

A. \( 3a + 2b - c + 2d = 0 \)  
B. \( a - 2b + c - 3d = 0 \)  
C. \( 5a + 10b + 6c + 4d = 0 \)  
D. \( 2a - 13b + 5c - 4 = 0 \)  

Bài tập: Cho hình lập phương \( ABCD.A'B'C'D' \) có tâm \( O \). Gọi \( I \) là tâm của hình vuông \( A'B'C'D \), \( M \) là điểm thuộc đoạn \( OI \) sao cho \( MO = 2MI \). Khi đó \(\cos\) của góc tạo bởi mp \((MAB)\) và \( (MC'D') \) bằng:  

\(A.  \frac{6\sqrt{85}}{85} \quad  B.  \frac{7\sqrt{85}}{85} \quad  C.  \frac{17\sqrt{13}}{65} \quad  D.  \frac{6\sqrt{13}}{65} \)  

1)  \(  
\begin{cases}  
\Delta \text{ qua } A \\  
\Delta \perp d  
\end{cases}  
\Rightarrow \Delta \subset \text{mp}(P) \text{ qua } A \text{ và } \text{mp}(P) \perp d  
\)  

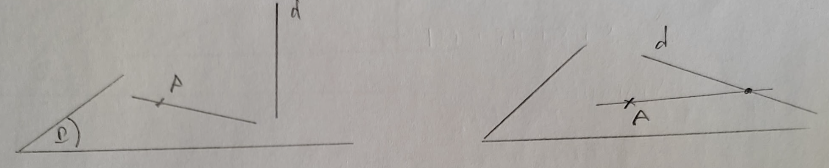
2)  \(  
\begin{cases}  
\Delta \text{ qua } A \\  
\Delta \text{ cắt } d  
\end{cases}  
\Rightarrow \Delta \subset \text{mp}(A, d)  
\)  

3)  \(  
\begin{cases}  
\Delta \text{ qua } A \\  
\Delta \parallel \text{mp}(Q)  
\end{cases}  
\Rightarrow \Delta \subset \text{mp}(P) \text{ qua } A \text{ và } \text{mp}(P) \parallel \text{mp}(Q)  
\)  

4)  \(  
\begin{cases}  
\Delta \text{ cắt } d_1 \\  
\Delta \parallel d_2  
\end{cases}  
\Rightarrow \Delta \subset \text{mp}(P) \text{ chứa } d_1 \text{ và } \text{mp}(P) \parallel d_2  
\)

5)  \(  
\begin{cases}  
\Delta \text{ cắt } d \\  
\Delta \perp \text{mp}(P)  
\end{cases}  
\Rightarrow \Delta \subset \text{mp}(Q) \text{ chứa } d \text{ và } \text{mp}(Q) \perp \text{mp}(P).  
\)  

6)  \(  
\begin{cases}  
d \perp \vec{a} \\  
d \perp \vec{b}  
\end{cases}  
\Rightarrow \vec{u}_d = [\vec{a}, \vec{b}].  
\)  

Bài tập: Đường thẳng \( \Delta \) giao tuyến của hai mặt phẳng:  
\( (P): x - 3y + 2z - 1 = 0 \),  \( (Q): 2x + y - 2z + 3 = 0 \)  
có phương trình là:  

A. \( \frac{x}{4} = \frac{y - 1}{6} = \frac{z - 2}{7} \)  
B. \( \frac{x}{4} = \frac{y + 1}{6} = \frac{z - 2}{7} \)  
C. \( \frac{x}{4} = \frac{y - 1}{6} = \frac{z - 3}{7} \)  
D. \( \frac{x}{6} = \frac{y - 1}{4} = \frac{z - 2}{7} \)