Áp dụng tích phân tính diện tích và thể tích - bài tập phần 13
Thể tích của vật thể tròn xoay
* Xét hình phẳng giới hạn bởi các đồ thị \( y = f(x) \), \( x = a \), \( x = b \) và \( Ox \)
Quay hình phẳng này quanh trục \( Ox \) tạo thành một vật thể tròn xoay. Thể tích của vật thể tròn xoay này là:
\( V = \pi \int_{a}^{b} [f(x)]^2 \,dx = \pi \int_{a}^{b} y^2 \,dx \)

* Xét đồ thị cong \( x = g(y) \), hàm \( g(y) \) liên tục trên \([a, b]\) và các
đồ thị \( y = a \), \( y = b \) và \( x = 0 \). Hình phẳng giới hạn bởi 4 đồ thị trên
quay quanh \( Oy \) tạo thành một vật thể tròn xoay có thể tích.
\( V = \pi \int_{a}^{b} x^2 \, dy = \pi \int_{a}^{b} [g(y)]^2 \, dy. \)

page 64
* Vấn đề:
Tính thể tích vật thể tròn xoay do hình phẳng sau quay quanh \( Ox \) tạo nên.

\( V = \pi \int_{a}^{b} \left[ (f(x))^2 - (g(x))^2 \right] dx. \)
b) Quay quanh \( Oy \)
\( V = \pi \int_{a}^{b} \left[ (g(y))^2 - (f(y))^2 \right] dy \)

page 65
* Nhắc lại đồ thị của một số hàm số cần lưu ý
1) \( y = a^x \)

2) \( y = \log_a x \)

page 66
3) \( y = \sqrt{a^2 - x^2} \) \( y = -\sqrt{a^2 - x^2} \) \( a > 0 \)
\( \Leftrightarrow \begin{cases} y \geq 0 \\ x^2 + y^2 = a^2 \end{cases} \) \(\begin{cases} y \leq 0 \\ x^2 + y^2 = a^2 \end{cases} \)
4) \( y = b \sqrt{1 - \frac{x^2}{a^2}} \) \( y = -b \sqrt{1 - \frac{x^2}{a^2}} \) \( a, b > 0 \)
\( \Leftrightarrow \begin{cases} y \geq 0 \\ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \end{cases} \) \(\begin{cases} y \leq 0 \\ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \end{cases} \)
page 67
\( y = x^2 - x + 3 \) và \( y = 2x + 1 \)
(2014.A)
page 68
(Tốt nghiệp PT 2006)
page 69
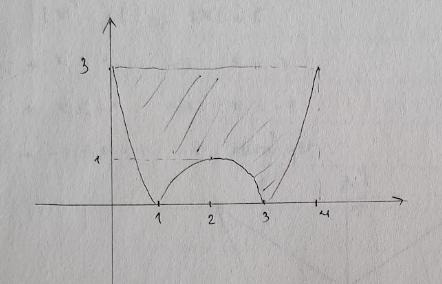
\( y = |x^2 - 4x + 3| \), \( y = 3 \)
(ĐHSP HN 2000 B-Đ)
page 70
\( y = |x^2 - 1| \) và \( y = |x| + 5 \)
(ĐHSP HN 2000)