Phương trình mặt cầu - Bài tập phần 3

Beedemy

Trang chủ

Bài viết

Phương trình mặt cầu - Bài tập phần 3

Bài tập: Trong không gian Oxyz cho mặt cầu \( (S): (x-1)^2 + (y-3)^2 + (z-2)^2 = 1 \) và hai mặt phẳng \( (P): x-y+z-1=0 \), \( (Q): x+y-z-3=0 \). Viết phương trình mặt phẳng \( \alpha \) chứa giao tuyến của mặt phẳng \( P \) và mặt phẳng \( Q \), đồng thời tiếp xúc mặt cầu \( (S) \).

A. \( x - 2 = 0 \quad \) B. \( x - y - 2 = 0 \quad \) C. \( 2x - y + 1 = 0 \quad \) D. \( x - 2y = 0 \)

Đáp án:

Mặt phẳng \( \alpha \): \( x-y+z-1 + m(x+y-z-3) = 0 \)
\( (1+m)x + (3m-1)y + (1-m)z -1 - 3m = 0 \)

Mặt phẳng \( \alpha \) tiếp xúc \( (S) \iff d(I, \text{mp} \alpha) = 1 \text{ với } I(1,3,2) \)

\(\iff \frac{|1+m + 3(m-1) + 2(1-m) -1 -3m|}{\sqrt{(m+1)^2 + (m-1)^2 + (1-m)^2}} = 1 \)

\( \iff \frac{|-1-3m|}{\sqrt{3m^2 - 2m + 3}} = 1 \iff m^2 + 2m + 1 = 3m^2 - 2m + 3 \)

\( \iff 2m^2 - 4m + 2 = 0 \iff m = 1 \)

Mặt phẳng \( \alpha \): \( x - 2 = 0 \Rightarrow \boxed{A} \)

page12

Bài tập: Mặt phẳng \( (): 2x + 2y - z - 4 = 0 \) cắt mặt cầu \( (S): x^2 + y^2 + z^2 - 2x + 4y - 6z - 11 = 0 \) theo giao tuyến là một đường tròn có bán kính \(r\) bằng:

A. \( r = 3 \quad \) B. \( r = 4 \quad \) C. \( r = 5 \quad \) D. \( r = \sqrt{34} \)

Đáp án:

Mặt cầu \( (S) \) có tâm \( I(1, -2, 3) \), \( R = \sqrt{1+4+9+11} = 5 \).

\( r = \sqrt{R^2 - IH^2}, \quad IH = d(I, \text{mp} P) = \frac{|2-4-3-4|}{3} = 3 \)

\( r = \sqrt{R^2 - IH^2} = 4 \Rightarrow \boxed{B} \)

page13

Bài tập: Cho mặt cầu \((S): x^2 + y^2 + z^2 - 2x + 4y + 2z - 18 = 0\) và đường thẳng \(d: \frac{x+3}{-1} = \frac{y}{2} = \frac{z+1}{2}\). Biết đường thẳng \(d\) cắt mặt cầu \((S)\) tại 2 điểm \(M\) và \(N\). Độ dài đoạn \(MN\) bằng:

A. \(\frac{\sqrt{30}}{3} \quad \) B. \(\frac{20}{3} \quad \) C. \(\frac{16}{3} \quad \) D. \(8\)

Đáp án:

\(MN = 2HM = 2\sqrt{R^2 - d^2} , d = d(I, d) \)

Mặt cầu \( (S) \) có tâm \( I(1, -2, -1) \) và \( R = 2\sqrt{6} \)

Đường thẳng \( d \) qua \( M(-3, 0, -1) \), \( \vec{u}_d = (-1, 2, 2) \)

\( d(I, d) = \frac{\left|[\vec{u}_d ,\vec{IM}]\right|}{|\vec{u}_d|} \)

\( \begin{cases} \vec{u}_d = (-1, 2, 2)\\ \vec{IM} = (-4, 2, 0) \end{cases} \Rightarrow [\vec{u}_d , \vec{IM}] = (-4, -8, 6) \)

\( d(I, d) = \frac{\sqrt{16 + 64 + 36}}{\sqrt{9}} = \frac{\sqrt{116}}{3} \)

\( MN = 2\sqrt{24 - \frac{116}{9}} = \frac{20}{3} \quad \Rightarrow \quad \boxed{B} \)

Cách 2: \( (-3 - t)^2 + (2t)^2 + (-1 + 2t)^2 + 6 + 2t + 8t - 2 + 4t - 18 = 0 \)

\( \iff 9t^2 + 16t - 4 = 0 \quad \Rightarrow \quad \begin{cases} t = -2 \\ t = \frac{2}{9} \end{cases} \)

\(M(-1, -4, -5) \quad \text{và} \quad N\left(\frac{-29}{9}, \frac{4}{9}, \frac{-5}{9}\right) \)

\(MN = \frac{20}{3}\)

page14

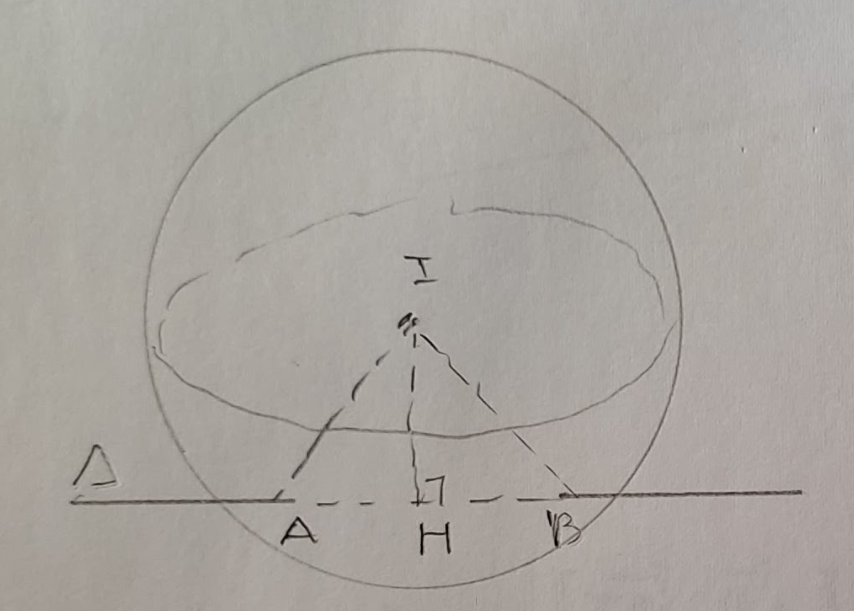
Bài tập: Cho điểm \( I(1, 0, 0) \) và đường thẳng \( \Delta: \frac{x-1}{1} = \frac{y-1}{2} = \frac{z+2}{1} \).
Viết phương trình mặt cầu \( (S) \) tâm \( I \) cắt đường thẳng \( \Delta \) tại 2 điểm \( A, B \) sao cho \( \Delta IAB \) đều. Bán kính bằng:

A. \( \frac{2\sqrt{15}}{3} \quad \) B. \( \frac{\sqrt{15}}{3} \quad \) C. \( \frac{\sqrt{6}}{3} \quad \) D. \( \frac{2\sqrt{6}}{3} \)

Đáp án:

\(\Delta\) qua \(M(1, 1, -2)\) và \(\vec{u}_\Delta = (1, 2, 1)\)

\( d(I, \Delta) = \frac{\left|[\vec{IM} , \vec{u}_\Delta]\right|}{|\vec{u}_\Delta|} = \sqrt{5} \)

\(\Delta IAB\) đều \(\iff IH = \frac{R\sqrt{3}}{2} = \sqrt{5} \iff R = \frac{2\sqrt{5}}{\sqrt{3}}\)

\((S): (x-1)^2 + y^2 + z^2 = \frac{20}{3} \Rightarrow \boxed{A}\)

\(\Delta IAB\) vuông?

\( d(I, \Delta) = \frac{R\sqrt{2}}{2} = \sqrt{5} \iff R = \sqrt{10} \)

page15

Bài tập: Viết phương trình mặt cầu có tâm \( I(2, 3, -1) \) và cắt đường thẳng \( \Delta: \frac{x+1}{1} = \frac{y-1}{-4} = \frac{z}{1} \) tại 2 điểm \( A, B \) sao cho \( AB = 16 \).

Đáp án:

\( \Delta \) qua \( M(-1, 1, 0) \), \( \vec{u}_\Delta = (1, -4, 1) \).

\( d(I, \Delta) = \frac{\left|[\vec{IM} , \vec{u}_\Delta]\right|}{|\vec{u}_\Delta|} = 2\sqrt{3} \implies IH \) , \( AB = 16 \iff HA = 8 \)

\( R = \sqrt{IH^2 + HA^2} = \sqrt{12 + 64} = \sqrt{76} = 2\sqrt{19} \)

\( (S): (x-2)^2 + (y-3)^2 + (z+1)^2 = 76 \)

page16