Bài tập: Cho mặt cầu \( (S): (x - 3)^2 + (y + 1)^2 + z^2 = 9 \) và 3 điểm \( A(1, 0, 0), B(2, 1, 3), C(0, 2, -3) \). Biết rằng tập hợp các điểm \( M \) thuộc mặt cầu \( (S) \) thỏa mãn điều kiện: \( MA^2 + 2MB \cdot MC = 8 \) là một đường tròn. Bán kính \( r \) của đường tròn này là:  

A. \( r = \sqrt{7} \quad \) B. \( r = 2\sqrt{2} \quad \) C. \( r = \sqrt{2} \quad \) D. \( r = 7 \).  

Bài tập: Trong không gian \( Oxyz \), cho mặt cầu \( (S): (x - 2)^2 + (y - 1)^2 + (z - 1)^2 = 9 \) và \( M(x_0, y_0, z_0) \) thuộc \( (S) \), sao cho \( A = x_0 + 2y_0 + 2z_0 \) đạt giá trị nhỏ nhất. Khi đó, \( x_0 + y_0 + z_0 \) bằng:  

\( A. 2 \quad B. -1 \quad C. -2 \quad D. 1 \)  

Bài tập: Gọi \( (S) \) là mặt cầu qua 2 điểm \( A(1, 2, 1) \), \( B(3, 2, 3) \), có tâm thuộc mặt phẳng \( (P): x - y - 3 = 0 \), đồng thời có bán kính nhỏ nhất. Tính bán kính \( R \) của mặt cầu \( (S) \).

\( A. 1 \quad B. \sqrt{6} \quad C. 2 \quad D. 2\sqrt{2} \).  

Bài tập: Trong không gian \( Oxyz \), cho \( A(0, 1, 1) \), \( B(3, 0, -1) \), \( C(0, 21, -19) \), và mặt cầu \( (S): (x - 1)^2 + (y - 1)^2 + (z - 1)^2 = 1 \). \( M(a, b, c) \in (S) \) sao cho \( T = 3MA^2 + 2MB^2 + MC^2 \) đạt giá trị nhỏ nhất. Tính tổng \( a + b + c \) bằng:

\(A. 0 \quad B. 12 \quad C. \frac{12}{5} \quad D. \frac{14}{5} \)

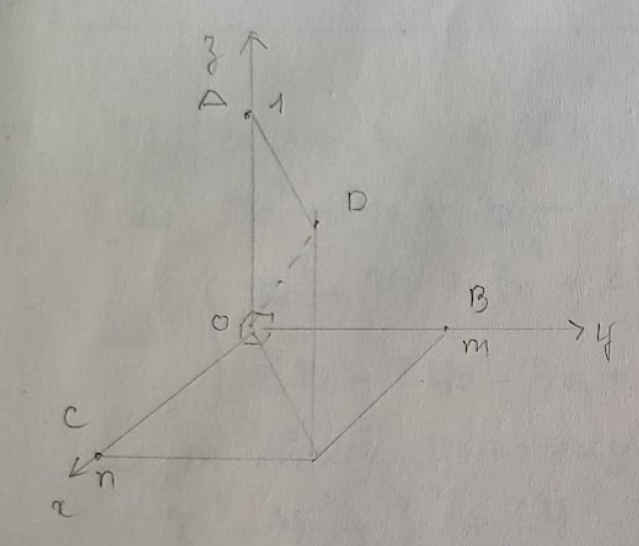
Bài tập: Trong không gian \( Oxyz \), cho \( A(0, 0, 1) \), \( B(0, m, 0) \), \( C(n, 0, 0) \), \( m, n \) là các số thực dương thỏa mãn: \( m + 2n = 1 \). Tính giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện \( OABC \).  

\( A. \frac{\sqrt{6}}{4} \quad B. \frac{\sqrt{3}}{3} \quad C. \frac{\sqrt{30}}{10} \quad D. \frac{\sqrt{3}}{10} \).